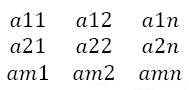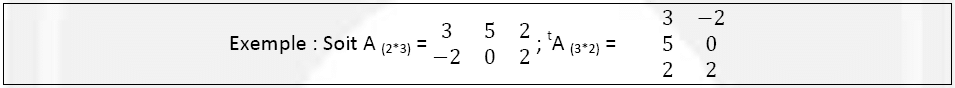|
Disponible en téléchargement |
Word 97/2003 |
Word 2007 |
|
|
|
|
|
Contrôle de gestion
Chapitre 1 : Gestion de la production
Partie 1 : Calcul matriciel
1.1.1 Définitions
Une matrice est un ensemble d’éléments disposé en lignes et en colonnes. Une matrice notée, A, d’ordre (m * n) est un tableau d’éléments formant m lignes et n colonnes. Chaque élément de ce tableau sera noté par aij où i désigne la ième ligne et j désigne la jème colonne. Mathématiquement, on peut écrire une matrice de la façon suivante :
A = (aij) ou [aij] ; i = 1, 2, …, m j = 1, 2, …, n
Exemple : A (3*2) =  |
ou
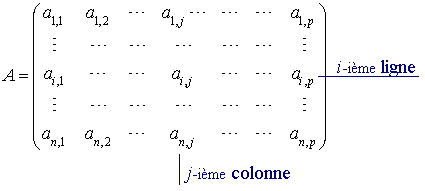
Soit deux entiers n et p supérieurs ou égaux à 1. On appelle matrice de à coefficients dans K, un tableau rectangulaire à n lignes et p colonnes d’éléments de K. On dit aussi que A est une matrice n x . Un tel tableau est représenté de la façon suivante :
Remarque : En fait, si on désigne par I l’ensemble des entiers compris entre 1 et n et par J l’ensemble des entiers compris entre 1 et p, se donner une matrice revient à se donner une application de I x J dans K, le coefficient ai,j représentant l’image du couple (i,j) par cette application.
1.1.2 Cas particuliers
Matrice carrée : m=n
Matrice diagonale : Une matrice carrée est dite diagonale si tous les éléments situés hors de la diagonale principale sont nuls. La diagonale principale est de haut en bas de gauche à droite.
Matrice identité noté par I: est une matrice diagonale dont les éléments diagonaux sont égaux
Matrice transposée de A est notée t A : est une matrice formée à partir de A en inter changeant des lignes et les colonnes.
Matrice ligne (ou vecteur ligne) : m =1 et n quelconque.
Matrice colonne (ou vecteur colonne) : n=1 et m quelconque.
