Cours DCG – Contrôle de gestion – Chapitre 1, Gestion de la production – Partie 2, Opérations sur les matrices

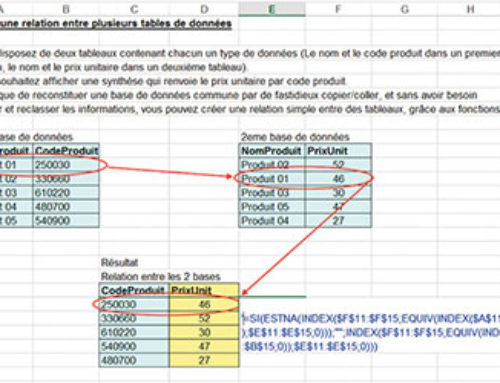
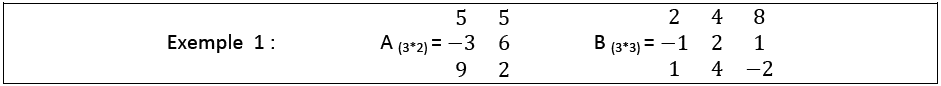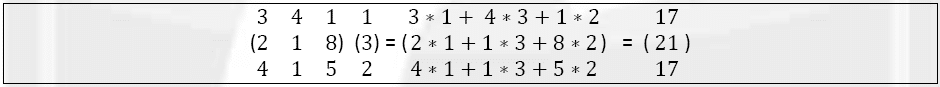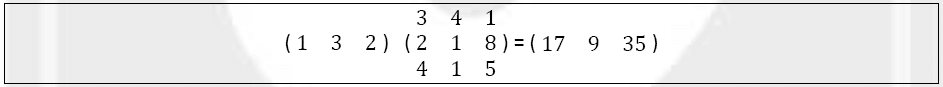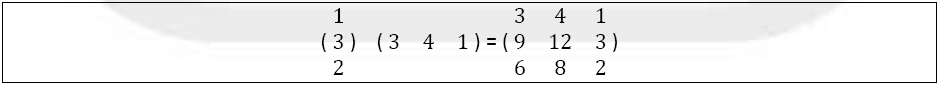Disponible en téléchargement	Word 97/2003	Word 2007	PDF

 

Contrôle de gestion

Chapitre 1 : Gestion de la production

Partie 2 : Opérations sur les matrices

 

1.2.1     Additions et soustractions de matrices

Ces opérations ne concernent que les matrices de même ordre. On additionne ou soustrait les éléments correspondants de chaque matrice.

 

1.2.2     Multiplication d’une matrice par un scalaire (ou nombre réel)

Soit A = (a_ij)        ; i = 1, 2, …, m                    j = 1, 2, …, n

Soit k un scalaire, alors k A = (ka_ij)

 

1.2.3     Multiplication de matrices

Le produit de deux matrices A et B existe si le nombre de colonnes de la première matrice A est égal au nombre de lignes de la deuxième matrice B.

C _m*n = A _m*k x B _k*n

On ne peut multiplier que B*A car 3 colonnes de B = 3 lignes de A

 

Exemple  3 : Produit d’une matrice par une matrice colonne donne une matrice colonne

Exemple  4 : Produit d’une matrice ligne par une matrice donne une matrice ligne

Exemple  5 : Produit d’une matrice ligne par une matrice colonne donne un nombre.

Exemple  6 : Produit d’une matrice colonne par une matrice ligne donne

Exemple  7 : Produit une matrice par la matrice identité donne la même matrice

Conclusion: A * I = I * A = A

 

1.2.4     Puissance d’une matrice

A_n = A*A*…*A

Calculer A² et A³ et A²⁰⁰⁹

A² = A*A

A³ = A² * A = 2A*A = 2A² = 2*2A

 

 

 

 

[spoiler effect=”slide” show=”Sous-Chapitres” hide=”Masquer”]

 

[/spoiler]